2014年5月21日 星期三

周夢蝶，唐文標 ( 1936~1985 )



昨夜，我又夢見我
赤裸裸地趺坐在負雪的山峰上。
　
這裏的氣候黏在冬天與春天的接口處
（這裏的雪是溫柔如天鵝絨的）
這裏沒有嬲騷的市聲
只有時間嚼著時間的反芻的微響
這裏沒有眼鏡蛇、貓頭鷹與人面獸
只有曼陀羅花、橄欖樹和玉蝴蝶
這裏沒有文字、經緯、千手千眼佛
觸處是一團渾渾莽莽沉默的吞吐的力
這裏白晝幽闃窈窕如夜
夜比白晝更綺麗、豐實、光燦
　
而這裏的寒冷如酒，封藏著詩和美
甚至虛空也懂手談，邀來滿天忘言的繁星……
　
過去佇足不去，未來不來
我是「現在」的臣僕，也是帝皇。
-----孤獨國/周夢蝶





周夢蝶詩人藏身在台灣的文藝復興萌芽前，他是市廛中一顆十足熠熠發光的明星！----張香華
女詩人張香華老師來電：秀堂，日前寄給妳的文稿，今日聯合報刊出，可以在臉書張貼了。
謝謝香華，詩人寫詩人，果然不同凡響，全文如下：

芒鞋破缽無人識──孤獨國周夢蝶不孤獨 ◎文/張香華 周夢蝶 照片/莊靈 攝影
聯合報─2014.05.22
〈文學紀念冊──詩人周夢蝶〉

有時我們幾個人在周詩人書攤擺龍門陣，忽然來了一位十八、九歲的女大學生左呼右喚叫他夢蝶！夢蝶！……霎時，我們像是看見一隻彩色斑斕的彩蝶在嫩黃的花蕊間翩翩飛舞……
今年，春雨方歇，時序進入五月第一個日子，一早發現台灣的各個媒體用特大的標題登出了一則新聞：詩人周夢蝶辭世，享年九十四……我擱下報紙倚在窗前，望見園中那株幾天前還盛開的薔薇，今晨竟落英遍地了。

認識周夢蝶詩人，是上個世紀中葉的事。那時台北沒有「誠品」，卻有一條全部開著書店的長街──重慶南路。從出版未成年少兒書的「東方出版社」，到挾「王雲五」重名、歷史悠久的「商務印書館」，街道兩旁密密麻麻開設著各式各樣的書店。

逛書店、聞書香，是台北文化人生活很重要的節目。就在這條長街中間，橫岔出一條側路──武昌街，有一家由俄羅斯人開的麵包店「明星」，一樓專賣西點麵包， 二、三樓是咖啡館，最具特色的是它那裝潢風味不同於一般店家的廊柱下，有位乾乾瘦瘦的男子在擺書攤，書攤的主人就是當時已頗有文名的詩人周夢蝶。就這樣， 上世紀六O年代，台灣在她蟄伏而幽閉的世界裡──那時是戒嚴時期，外來資訊幾近被阻絕，而另一方面，經過從大陸退守到台灣二十年的休養生息，島內的生命力 已蓄積到一定的飽和點，一顆小小的露珠，晶瑩剔透，就會折射出萬丈光芒，周夢蝶詩人藏身在台灣的文藝復興萌芽前，他是市廛中一顆十足熠熠發光的明星！

何以會把他和文藝復興氣息相連接，要從周夢蝶詩人擺攤賣書的地理位置分析說起，詩人書攤方圓一公里之內，全是當年（或早年）具有權勢，金融與文化制高點的 建築物：重慶南路上有自日據時代到今天都仍是最高權位的總統府（當年稱總督府），有最大金庫的台灣銀行，其東是文化蘊藏深厚的台灣第一所博物館，對面是豎 起希臘神殿式七根宏偉圓柱的土地銀行，北有古樸又氣派的台北火車站，對街是最具規模的台大醫學附設醫院……這些巍峨的建築物全是日據時代建築完成的，而且 一律採用歐洲古典巴洛克風格，詩人的書攤就隱身其中。但他特立獨行，完全無視於附近任何一攤生意的蓬勃與興隆──其實每一個攤位的牌照已價值不菲，別人的 書攤都經營得五花八門，賣的東西包羅萬象，唯獨詩人的書攤例外，他永遠只賣封皮破損。紙張陳舊的冷門詩集、文史、哲學一類書籍。因為詩人的心老早穿梭過宏 偉又高聳的梁柱，他抬頭看著飛鳥在上面築巢或餵食雛鳥，他的靈魂終日徘徊在博物館的廊柱間，瀏覽著綠樹成蔭、花葉扶疏的台北市新公園……這麼超凡脫俗的環 境，詩人的耳朵也老早飛到公園裡那個設有貝殼型舞台的露天音樂廳，他傾聽著飛鳥向青空放歌去了！對營生本來就缺乏興趣的詩人周夢蝶，難怪對書攤生意的經營 會愈發一天打魚三天曬網了啊！

造成詩人不事生產還有另一項重要因素，是他往來的全都是一些「清談誤國」的文士，平日多靠煮字療飢維生，沒有固定的上下班時間。而飲茶喝咖啡的消費又列不 入文人寒士的生活預算裡（正確的說，那年頭咖啡還沒有普遍登陸台灣），登堂入室上二、三樓喝明星的咖啡簡直是奢侈的敗家行徑，所以到武昌街找明星咖啡館門 口的詩人聊天，就成了最實惠又風雅的時尚。經常見到三兩個人坐在明星咖啡廊前，圍住詩人談詩說藝論紅樓……不知覺間常常一抬頭才發現天色已暮。──這幕景 象十足是台北當年的文化風景！少了這一塊，那年頭的台北文化拼圖就不算完整。
〈孤峰頂上〉是我認為詩人一生的力作，筆力堅厚飽滿，意境高遠卓絕，很能代表詩人一生的堅持和苦行修練的功夫。

恍如自流變中蟬蛻而進入永恆
那種孤危與悚慄的欣喜！
彷彿有隻伸自地下的天手
將你高高舉起以寶蓮千葉
盈耳是冷冷襲人的天籟。
擲八萬四千恆河沙劫於一彈指！
靜寂啊，血脈裡奔流著你
當第一瓣雪花與第一聲春雷
將你底渾沌點醒──眼花耳熱
你底心遂繽紛為千樹蝴蝶。
……
想六十年後你自孤峰頂上坐起
看峰之下，之上之前之左右。
簇擁著一片燈海──每盞燈裡有你。

任誰讀了這首詩都會冷然又肅然，就像自己正站立在高高的孤峰頂上屏氣凝神萬念俱寂，不敢出一口大氣一樣！
那時我正在師大面臨畢業讀大四，同系中有位好友「連」因為住在詩人書攤的附近，上學前常繞到書攤上邀詩人周夢蝶一起去旁聽一堂熱門的哲學課，反正他經常都 把書晾在地上，跟朋友四處漫遊！那天，我也正要出門去上課，忽然接到「連」氣急敗壞打給我的一個電話，她告訴我她再也不去上這門課了。我問她發生了什麼 事，她說她剛接到另一個同學的口訊，原來周公（那時我們都背地裡稱呼他「周公」）託人問「連」到底對他存什麼意思！後來我目睹「連」漲紅臉斥責詩人周夢蝶 的那一幕，「連」瞪起杏眼：「有什麼意思？有什麼意思？你自己說呀！自己丟臉也就算了，還丟到我的同學那邊去！」周詩人的臉上頓時一塊青一塊白，好不難 堪！事隔多年之後，我們聽到另一個笑話，那是另一位女詩人在遠渡重洋赴美留學之前，周詩人這回果然不託他人而親自表白，他直截了當的問：「妳願不願意嫁給 我？」答案是：「神經病！」我們只好嘆一口氣：詩人對現實生活的了解實在是太「超現實」了！
剛認識詩人周夢蝶時，就聽他常引用佛家經典，我很自然的把他和民國初年的數度出家又還俗的蘇曼殊聯想在一起，蘇有首纏綿的〈本事詩〉：「烏舍凌波肌似雪， 親持紅葉索題詩。還卿一缽無情淚，恨不相逢未剃時！」既而知道周詩人本名周起述，自取筆名夢蝶，頗見嚮往莊生了悟生死的大智大慧之意，油然生出崇仰之心。 有時我們幾個人在周詩人書攤擺龍門陣，忽然來了一位十八、九歲的女大學生左呼右喚叫他夢蝶！夢蝶！……霎時，我們像是看見一隻彩色斑斕的彩蝶在嫩黃的花蕊 間翩翩飛舞……而現在，山谷中空留蝶痕，周詩人顯然是去和天上的莊生論道去了！
●作者按：本文標題語出蘇曼殊〈本事詩〉：春雨樓頭尺八簫，何時歸看浙江潮？芒鞋破缽無人識，踏過櫻花第幾橋。
【2014/05/22 聯合報】




 這篇，或沒引用周夢蝶的詩的報導，都不值得看的。
官方說法等，更肉麻，省省吧。
謹記去年的會面：0323 2013 遇 見 周夢蝶先生

也許近3點40分鐘，仔細看完『周夢蝶手稿暨創作文物展』(背景聲音是周先生唸其作品，當時還可算鏗鏘有力。)

我剛走出門，看到幾位老師推著輪椅上的周先生 (92歲) ，從印度黑檀樹蔭下，逼進來。三位老師將其提起來，越過二節石階，走上展覽場 (幾乎所有的人窩的，都是瑣碎的言語。在會場聽演講者大談諸如『論周夢蝶的死亡意識』等議題，而周先生炯炯有神地端視著我這位陌生人。

將周先生送進場，扶他到座椅時，就開始許多同學照相。周先生很機伶，示意他要在展覽簽名簿上簽名。然後，他一筆一畫地寫小字簽名，當然不是展覽會上的書法水準，不過字跡可辨。

然後他回去原位，又示意他想坐到另外一張垂直方向靠牆壁的椅子。接下來周先生很平靜地面對五六部相機，老師們也一一像某張「孫逸仙坐蔣介石站」(偽照片)的姿態照相。

展覽會場有王曼文選周先生的詩句，作成書籤『向萬里無寸草處行腳』、背面是印光法師的話：『欲真利人，當事事盡己之分，則日用行為，皆含化人之機，久而久之，人自見信而依從之，固有不期而然者也。』……


***
這是 文學評論家唐文標先生 ( 1936年2月2日~1985年6月10日 ) 於1984年( 月日不詳 ) 給向陽的信，推薦楊君詩作及其舊作給《陽光小集》。信文如下：
　
向陽兄：
久不見 . 念 . 自立間看 . 老弟衝勁仍足至賀 . 近身體不真甚佳很少外出 . 故少聯絡耳 .
友人楊君初作新詩 . 余以為不妨發表 . 公如當新人佳作處理之於「陽光小集」極善 .
某之詩生活一文發表 . 人多不識某亦曾寫過詩者 . 思之愧甚 . 若陽光欲化篇幅將某昔年舊作 ( 如公無渡河 . 越絕 幾首 ) 登之載之 . 以塞悠悠之口 . 則亦妙事也 .
匆匆 . 即奉
近安 唐文標 敬



唐文標自撰簡介稿
　
唐文標 民國25年2月2日生
廣東省開平縣人. ( 男 )
B.A. University of California. Berkeley, U.S.A.
M.A.
Ph.d University of Illinois, Urbana, Ill, U.S.A.
著作；1.平原極目. 4. 唐文標碎雜 .
2.天國不是我們的. 5. 我永遠年輕.
3.快樂就是文化, 6. 張愛玲研究.
7.張愛玲雜碎 8.中國古代戲劇史初稿.
9.張愛玲資料大全集 10.唐文標散文集.
現任： 國立政治大學教授.
地址：木柵國立政治大學數學系.
電話. ( 04-2518045 )

唐文標（1936年－1985年），數學家，詩人，文學評論家。

[編輯] 生平

1973年，臺灣大學數學系客座教授唐文標先後在《龍族詩刊》「評論專號」、《文季季刊》及《中外文學》發表〈什麼時候什麼地方什麼人——論傳統詩與現代詩〉、〈詩的沒落——臺港新詩的歷史批判〉、〈僵化的現代詩〉三篇文章，強調詩的健康特質，認為詩所別具的美好言語應該對社會引起正面作用，批判周夢蝶、葉珊（即台灣作家楊牧早年使用的筆名）、余光中等人對現實的逃避。隨後，顏元叔發表〈唐文標事件〉[1]加以反駁，因此這一次的論戰就被稱為「唐文標事件」。緊接著，余光中又發表了〈詩人何罪〉，批評唐文標思想危險：「滿口『人民』、『民眾』的人，往往是一腦子的獨裁思想；例子是現成的。不同的是，所謂文化大革命只革古典文化的命，而『僵』文作者妄想一筆勾銷古典與現代。這樣幼稚而武斷的左傾文學觀，對於今日年輕一代的某些讀者，也許尚有迷惑的作用。」並威脅《現代文學》之白先勇及姚一葦二教授，不准《現代文學》再發表任何唐文標的文章[2]。
1984年出版《中國古代戲劇史初稿》，同年邱守榕受聘彰師大。唐文標與邱守榕結婚，二人皆為數學家，有一子唐狷。1985年6月10日因鼻咽癌病逝於台中榮民總醫院。

[編輯] 注釋

  1. ^ 《中外文學》2卷5期，1973.10
  2. ^ 施善繼：〈鄉土文學論戰三十年〉

****

〈燃燒的年代〉──唐文標逝世２０周年紀念專輯

　陳映真

１９７１年，我住在一個孤單的外島上。幸運的是，我獲准訂閱兩種文學刊物，一是《幼獅文藝》，另一是《中外文學》。當時復刊的《文季》，也由家人寄來。
　　每月收到這些文學刊物，對當時枯索的生活，是一種莫大的心靈的滋潤和安慰。然而，也在這些文學刊物上，我聞到了外面世界巨大而激盪的變化。

點燃現代詩論戰

　　在《中外文學》上，出現了批判和反省臺灣現代詩的文章，不論在思想內容上，在文學的意念上，在方法和邏輯上，是臺灣戰後文學界，尤其是１９５０年以後的臺灣文學界裏不曾公開出現過的。我驚奇而且激動地讀著，我感受到七O年代臺灣思想和文化界一個重大的轉變。
　 　這些文章中，最受注目的，就是唐文標的《僵斃的現代詩》和其他的文章。我當時覺得他的這些文章，以及若干由海外知識份子寄回來的批評獨佔臺灣詩壇二十年 的「現代詩」的文章，雖然在整個中國新文學思潮中，不是新的東西，但在１９５０年以後隔離著一個中國新文學斷層的臺灣文壇上，卻是新的事物，有臺灣文學思 想史上的重大意義。而五、六年以後的《臺灣鄉土文學》論戰，其實便是這《現代詩論戰》的延長。離開唐文標點燃的現代詩論戰，就無從把握鄉土文學論戰的思 想、文化上的意義。 　　
　　唐文標是誰？
　　這是每次讀完唐文標的文章以後，禁不住要問的問題。當時，我離開臺灣才 四、五年，從前一向沒聽見過這個名字。但他卻顯然已經是《文季》的同人。

文章活潑詭奇，奔馳飛躍 　　

　　１９７５年，我回到台灣，在天驄兄家，見到了唐文標，開始了我們長年來的友情。
　 　唐文標，是一個臺灣制式教育絕難以培養出來的人才。他聰明、敏銳，才華橫溢。他的專業是數學。但他在批判理論、文學、戲劇、和其他人文科系上涉獵殊廣， 而且各有極為獨到的心得。南方朔就說過，唐文標在思想和治學上，是一個天才型的人物。他的文章活潑、詭奇、奔馳飛躍，閃耀著他內面的才情，和一般嚴謹苦思 以治學的人大不相同。如果唐文標的外務不那麼多，不那麼喜歡找朋友聊天，不那麼為朋友的苦樂分心，則他必然是一個能冶文學、思想、人文科學於一爐的宗師級 人物。 　　
　　唐文標一生熱愛朋友。他關心朋友在精神、物質上的困難。沒有人知道他為了朋友，散出了他私人多少金錢，花費了多少他寶貴的時間。 一直到他不幸罹患惡疾，他依舊那樣繁忙熱情地關心朋友的苦樂，給受挫的朋友打氣，給失望了的朋友以安慰，給徬徨苦悶的朋友找感情和思想的出路，弄得自己頭 痛、疲乏、精疲力盡。 國家的事，留給你們了！
　　１９８５年６月９日，我和天驄兄趕去台中榮總看他。那時他已做過氣管切開手術，不能言語。一見 了面，他就抓著紙和筆寫字和我們『聊天』。他告訴我他正在寫台灣文學史綱，尚未完成，目前正在寫五０年前後的一段。他另外寫著一部有關台灣清朝時代農民蜂 起的文章，據說有５萬多字，也尚未完工。他讓我覺得，他不安、遺憾，為了他許多想做的事，也為了他做了卻尚未完成的事。邱守榕大姐給我看前一夜送進開刀房 前的他的遺言。對他的父母姊姊，他說：『我愛你們，對不起你們。』留朋友的是───　　『親愛的朋友：國家的事，交給你們了。』
　　我讀著，眼眶濕了。
　 　他熱愛著中國。正是對中國的愛，使他從七０年代開始，就回到台灣來，在台灣生活、教書、工作、交朋友。保釣愛國運動，使海外知識份子一下子投入一個激盪 的時代。唐文標便是在保釣火焰中煅燒出來的人物。但保釣運動運迅速變化，從統運的高峰，跌落在分裂、絕望和幻滅的谷底。有不少人變得犬儒、有不少的人轉變 了方向。唐文標也和別人一樣經歷了希望和幻滅、經歷了勝利與挫折。但唐文標卻永遠沒有轉向，沒有撤退，沒有成為一個不但失落了理想，而且進一步為那理想初 心的敵對者。這自然有他內面天生的人格上的因素。但我想，這和唐文標決定把他生命的根堅毅地在台灣這這祖國的土地上落實，有很大的關係。理想，對於唐文 標，再也不只是在異國流浪的中國知識份子安慰寂寞情怯的工具，而是最具體實在的每天的工作，祖國和民族，對於唐文標，絕不只是流寓異鄉的知識人的感情上的 蔭庇，而是具體、現實的日常生活。
走得多麼的唐突
　　唐文標走了。走得多麼的唐突。知道這回住院，情況比往時都壞，但也絕不曾想到次日凌晨就和我們永別。唐文標只長我一歲。這是我猛然想到自己到了故舊開始凋零的年紀，想著唐文標走前壯志不酬的焦慮，想著自己陷身於生活泥沼中疲憊地掙扎著自己。也不免感到更深一層的孤單。
　　但，老唐阿。你的大去，又一度喚醒了我們。時日無多，待收的莊稼卻任它荒廢著。對於這樣懶惰的自己，不禁感到羞恥了。老唐，安息吧，我們會好好地振作起來，努力工作，說什麼也不能讓你再為祖國擔憂啊………

　　　您回來使睡夢的人驚醒，讓盲者開眼，
　　　　　叫迷失的時代找到方向，
　　　　　臨終留言：深以中國為憂
　　　您大去朋友震悼，讓伙伴悲泣，叫奔馳的歷史駐足，
　　　　　我們誓言：再不讓您為祖國擔憂
　　　　　　　　　　　　　　　　　　　　　　　　　　───陳映真

******
統計學淺談
唐文標



(甲) 統計要做什麼事

我們在一生之中，不是很喜歡詢問嗎：這是什麼東西？對我有什麼用呢？我們現在也不妨來問一問，統計是什麼東西，能幫助我們什麼呢？
沒有錯，大家都了解，統計可以說是數學的一支，用來研究數據現象的。這種現象當然是社會現象（包括自然現象），我們作為人居住在這世界上所碰到的問題，例如一年之間每一日的平均氣溫，或臺北市去年每一個市民的入息等等。
我們在這裏可能面對二個問題，第一個是這堆數據從那裏來的，就是說，這個現象是真的現象嗎？怎樣找出「數據」呢？第二個是這堆數據在說什麼？它對我們的生 活有什麼特別意義呢？這些無疑都是統計的問題，研究數據也是為了解決這類問題。所以，我們念統計的時候，難免要同時照顧兩方面的困難：一方面是本質問題， 統計能告訴我們那是什麼社會現象呢？另一方面是技巧問題，怎樣才能把社會現象的本質弄清楚，整理好，使人明白呢？要解決這二個困難建立了統計學，學習統計 學的主要目標也在研究這二種困難。我們這篇文字的論點更在嘗試，從這二個困難的解決過程中，了解統計的結構關係。或者可以說，統計的整個結構就在考慮這二 種困難的解答途徑中建立的。
也許在進一步提出觀點時，我們不妨先指出高深的統計，雖然是由這種困難的研究中出發，但高等統計還有別的難題，例如作統計推論、下判決、和預測的時候，我們還牽涉到應用一些信仰，一些原則，甚至一些經濟理論等問題，這裏姑且不先說明，機會到了我們再提出來檢討和分別清楚。
我們回到最原始的開始，假如我們要明白一個社會現況，或者是社會存在著一種迫人的現象，一定得要了解它的含義，那麼該怎麼辦呢？前者例如想 清楚知道目前社會的財富分配的情形如何？後者如世界連年乾旱，糧食歉收的現象所惹起的饑荒情形。這些切身而重要的問題，應用統計技巧無疑的是一個很好的途 徑。
我們提出一個「統計測度」的觀念。一方面希望用它來答覆上面的二個困難，另一方面也可以用來作整個統計結構的支柱。
因此，所謂「統計測度」，就在面對著一堆原始累積的資料。數據、現象……我們要用一二個簡單的統計量表達它的本質特性，這些統計量便是統計 測度。統計學要做的事，便是把這些測度找出來，用它解釋原來母體的現象的意義。不過，我們也得知道，這些測度也有它的極限，它並不能表達多過它本身所含的 統計意義，尤其得注意它的樣本裏面的代表性和隨機性的困難條件。在近代人亂用、妄用、誤用和濫用的方式下，統計測度大部份時間都是被人利用，來讀出不真實 的結果，這是應極為小心注意的。

(乙)統計測度

我們可以說，最少在基本統計學上，整個統計結構全建築在怎樣去找尋和認識這個「統計測度」的問題上。正如我們在批評人的時候，會說這個人是壞人，或這個人 喜歡食糖這類特性。統計測度的功用也在這裏，多少是用一種主觀的認知來論斷客觀的事實，不過，統計沒有像批評人時那麼多「價值判斷」──甚至「道德判斷」 而已。
一般情形是這樣子的：社會的現象，大部分是可以用由質化量的方法，轉換成一堆數據的；例如天氣的舒服程度可以用溫度計，氣壓表等等表示，而 一個人的社會地位，壞人好人程度也可以用他手上擁有的金錢數量來權衡，也是這種方式：由質化量。我們姑且從這裏開始，即是說，面對著一大堆今年全國民眾的 收入所得報告：張三四千，李四一萬之類，我們怎麼辦呢？全國同胞那麼多，我們不可能一一去訪問了解，我們只好選取跟我們有關，或我們想知道的問題，來找尋 數字的答案了。例如我要知道我的薪津所得，是否和大多數人所得相同呢？或者你要知道年薪四萬元的人數有多少，以便向他們推銷某種生產品。在這種情形考慮之 下，我們不必要知道每一個個人的年薪，而且通過這些個人收入來了解他和整個收入分佈的關係，更簡單地想，如果想明白某甲的實際情況，那麼可以直接找他，否 則，能不能夠用一二個數字來表現整體的一些觀念呢？我們通過整體的一些觀念來找尋這種數字，就是統計測度了。
這些數字，自然也不是普通的數字，而是統計量， 即是應用了所有母數整體的特性和數據的函數。所以， 測度雖只出現像一個數目，但卻盡可能包含了整體數據的某一性質， 我們要了解這個現象時，便轉移到要了解「測度」了。

(丙)敘述性統計測度

我們上面已說過從一堆數據內，找到一個函數，也是我們的統計量， 用它來解釋現象。我們這裏會問到二個問題：函數是怎樣子的呢？ 怎樣求得到這種函數呢？我們先舉例來說明函數的意義和應用範圍。
例如在一堆國民全年收入所得的數據中，我們如果要問： 用一個數字來表達整個收入所得的中心傾向，那麼該用什麼數字（測度）呢？ 差不多的問題也可以這樣問：如果選一個人來作代表（典型的納稅人也）， 那麼你猜他的一年收入多少呢？這個問題並不難見，但不易有一個完整的答案，有幾種常用的測度皆可以用來答這個問題。


(一)平均值：整體如果均勻分配，每一個成員應該分配得到的數目。

(二)中數：中間的數目，即是從小到大依次排列的中央值， （前面人數與後面人數相等的那個值。）

(三)眾數：最多出現的那個值。（最多人入息是那個數字的值）

(四)中距點：最大值和最小值的中點。
此外還有其他的測度，可以用來猜測度中心點何在，但我們不如用一實例來解釋它的用法。
例：一間公司成員有二十人，自小工友到大老闆，每月月薪有別：
職別 薪金 人數
工友 2000元 2
辦事員 3000元 8
店職員 4000元 6
經協理 10000元 3
老闆 100000元 1
計算一下，各種測度的實值是


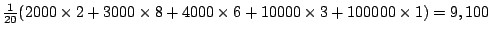(一)平均數： $\frac{1}{20}(2000 \times 2+3000 \times 8+4000 \times 6+10000 \times 3+100000 \times 1)=9,100$元

(二)中 數：在3000和4000之間，可以取3500元。

(三)眾 數：3000元。（人數為8，最多）

(四)中距數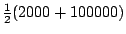： $\frac{1}{2}(2000+100000)$=51000元。
這些測度求法都不難，但要談到它的意義，以定取捨，卻很有商量餘地了。 因為每一測度，用來代表或解釋我們所有的現象的含義，一定有長處也有短處， 取捨之間，難免由於客觀的要求乃至於主觀的選擇了。
我們現在的問題如果定為：隨便挑選一個人，那麼他的薪金大概多少呢？


(一)如果只限制在這小公司中，那麼用「中數」最好。 只要比較一下中數和平均值數，很顯然， 平均數被大老闆的每月十萬元薪金所影響，未免太高了， 和佔有二十人中十五人相比，相差太遠了。反之中數值三千五百元， 很接近大多數人的實際收入。

(二)如果要求絕對準確，（相差一點和誤差很多都是一樣的）， 而且最大可能的，那麼眾數是最好的測度，因為那是最多出現的。

(三)如果長期計算，不限於大規模的幾個人，那麼因為有「扯平」 的平均原理存在，自然平均數比較好了。

(四)在數據量很大時，這四種測度都大致相等。但由於平均值容易計算，且由於它是完全照顧到所有數據的數值，因此頗適合其他統計原則的要求， 一般用得較多。
我們還有其他的各式各樣的測度，例如動差，方差（變異數），標準差， 相關係數等等。每一種測度都可以用來解釋和猜測數據所代表的那個現象母數的一些特性。例如「方差」這個測度， 計算時是代表每一數據和平均值（中點）的距離平方的總和數， 可以用來表示整列的數據和中心值（平均數）的離散情況，是不是普遍的離得太散， 還是集中在中心地帶呢？其他的測度大概都是用來解釋數據背後的現象的意義。 我們也可以想，假如數據是歷史事件， 那麼所謂測度不過是利用歸納方法，累積過去的經驗，來解釋歷史事件， 與及歷史變化的規律，甚至進一步推論歷史的方向。
我們目的正在這裏。一方面我們總結過去的知識，整理過去的經驗， 然後學習了過去的教訓，另一方面，進一步我們要詢問了我們知道這些事以後，能做什麼呢？究竟，統計能帶給我什麼呢？要對我說何樣話？
在以前的例子來說，比方說，我們已知每人薪金平均數為9100元， 中數為3500元之類，我們能做什麼？我們可以設想多一點， 若這二十個人不是從某一公司出來人，其實是一個典型的抽樣， 這二十人是整個社會的一個代表性範本，那麼我們能否由這二十個人的出現， 或者由他們的薪水所得，推論整個社會的薪水所得呢？ 學統計的意義和目的正在這裏。歸納本身自然有它的意義， 但我們還可以進一步看，尤其是在我們無法統觀整個社會，了解現象， 甚至沒有能力獲得很多數據之前，我們只好作預測的工作，就是說， 我們要利用統計這個測度，從露出海面的十分之一冰山， 推測在海底十分之九的冰山形狀。這類工作目前有幾種想法，一般來說， 就是總數據結果，猜測一下整個大現象的意義 (例如從中數3500元猜測全部人口的月薪也是3500元)這種猜測難免有點冒失， 有時難免差得太遠。倒不是說它一定不準確，而是說它有很大機會不準確， 或者說這次準確後，下一次準不準確還是沒把握之類。為了這個緣故， 我們不得不進一步再研究一下這現象的處理和方法了。我們的問題有二個， 第一，這社會現象有沒有規律性？第二， 假如把現有的小現象作為未知的母數大現象的一個樣本， 我們能否依據所得來的測度，或者去求出一個運用這樣本的測度， 進一步估定出整個母數的測度。(例如用樣本平均數來推定母數的平均數)。 我們也可以這樣想，假使對母數的平均數有更多的訊息， 能否利用這個樣本來檢定這個母數平均數是否可以接受？ 我們甚至可以這樣想，我們面對一個全然無知的宇宙， 手頭所有的只是一些偷看天象的消息(樣本的數據)，我們要憑藉這些小消息 (樣本，或樣本出來的測度)，進一步下一個決定， 例如在什麼時候我們這樣做，在另一時候，我們那樣做，這一類東西。
為了解決這些問題，我們談一點解決它的技巧。

(丁)概率空間的意義：

我們先談第一個問題，就是現象所處身的，例如自然界，有沒有規則？ 社會發展是否可以找到一定的發展規律呢？我們自然不知道， 但嘗試去解釋它是一件人類的事，我們的想法是有時可以利用一個「數學模型」 來逼近解釋這社會現象的。
這裏，我們可以分開來說，這種假設是同時有理論性和經驗性的意義的。 下面希望能解釋這一點。
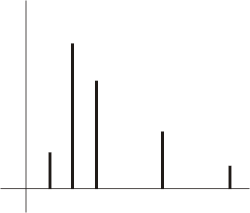
從前面舉例得知，20個人中月薪不齊。我們可以假設這是一個常態分佈函數，其密度函數是
\begin{displaymath} f(x)=\frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(X-\mu)^2}{2\sigma^2}} \end{displaymath}

其中μ和$\sigma^2$是二個參數的常數，(就是說服從一個數學模型了) 我們要利用樣本來推測μ和$\sigma^2$的真值。
但另一方面，由於20個人中月薪不齊，所以它形成某種經驗分佈(模型) 圖樣。例如由20人變為100人，那麼很可能有下面圖形，像跟據中心極限定理， 愈來愈接近一個理想型的分佈也。這就是經驗上趨近常態分佈的意義了。






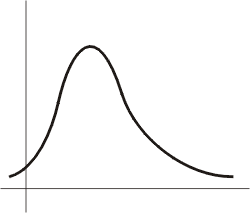我們想法是，統計基本設計是，利用一個概率模型來解釋世界。 例子中我們要問，這些月薪是否合乎一個概率空間（模型）。 一個人之入息服從某些定則？隨便拿起一份月息報告， 那麼這些所得的價值是某一數，是否服從某種概率分佈函數而出現的呢？ 如果是，那麼便可以用概率方法來討論了。
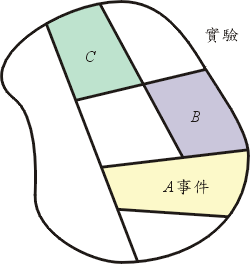
再舉一個例子。一間玩具工廠，可以出品多種不同的玩具。 我們可以稱每一次出品玩具的配合為「事件」。(例如，十隻玩具狗， 二十具坦克車為一個事件。)如果這些事件的出現是合於市場要求的， 因此具備了一條已客觀存在的概率函數的條件， 我們將這種條件和所有事件一起來想，這就是「概率空間」的起源了。
但是，事件可能是一種事實，一種實驗結果，或一些發展的種類， 不一定能適合運算，更無論從中找到數字測度了。例如在這種想法下， 說一個人窮不如說明他的入息是多少。為了這緣故，我們把事件量化為數據， 甚至進一步改訂「事件」。
改訂事件就引進了「隨機變數」這一個觀念。也是說用數學的語言來簡化 「概率空間」，使它更合於統計的運算。 改訂「事件」的過程是要詢問二個問題：

(一)某一事件是甚麼？

(二)某一事件有多大？
這就是我們對一個實驗中任一事件的態度，究竟這事件是什麼東西呢？ 實驗 問：A這「事件」出現的意義：

(一)它是什麼？

(二)它身體多大？



我們來答覆這二個問題。
(一)這事件是什麼？我們把它轉換一下(事實上， 也就加入了自己對這事件所加進去的要求或認知的範圍，也是說， 我們並不在乎對這事件完完全全的客觀了解， 只不過為自己興趣和目的而轉換而已。) 我們轉換這事件到可以使用數字來代替它，也許更簡單的說，是把這事件用 「數字」命名，或是化它為數字，因此我們不說天氣熱， 而說氣溫三十五度之類。數學化一點說，便是利用隨機變數這個函數， 把實驗的事件映射到實數系上面去。
(二)這事件有多大？當然大小是和全體相比而知道的。 我們可以計算這事件的概率，或者比較它佔全體的多少部份。更數學化一點， 利用一個概率函數，把這隨機變數的值全映射到0與1之間的實數集去。



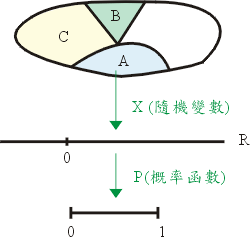舉例來說：拋二個銅板，結果可定為，
[梅，梅]，[蘭，梅]，[梅，蘭]，[蘭，蘭]。
每一對都是相等機會出現的。

(一)如果你要求的為出現蘭面的個數， 因此隨機變數X當然代表出現蘭面的個數，因此，X可以是0，1和2， 而它的概率相應為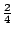$\frac{1}{4}$，$\frac{2}{4}$，和$\frac{1}{4}$

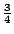
(二)如果你要求的是蘭面出現與否，因此隨機變數X當然代表出現蘭面時有一代號，(設為+3) 不出現蘭面時另有一數字代號，(設為-2)。 故X值為-2和+3，概率依次為$\frac{1}{4}$和$\frac{3}{4}$

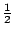(三)如果你要求的是二個銅板出現的面是否全同， 因此隨機變數X在出現二個梅面或二個梅面或二個蘭面時有一數字代號， (設為1)，否則二個不相同時也有一數字代號，(設為0)概率則是相同的， 都等於$\frac{1}{2}$。
這裏說明了因為要求不同，所訂出來的隨機變數的定義值改變了。 因而機率也改變了。 下面我們用一個例子來比較這些不同點，並進一步綜合隨機變數的結果為概率函數。

(戊)概率函數：

X 前面出現 概 最少出現 概 最多出現 概 面為全同 概
的次數 率 二次梅花 率 一次梅花 率 率
(梅,梅) X=0 $\frac{1}{4}$ X=2 $\frac{1}{4}$ X=0 $\frac{1}{4}$ X=1 $\frac{1}{4}$
(梅,蘭) X=1 $\frac{1}{4}$ X=0 $\frac{1}{4}$ X=1 $\frac{1}{4}$ X=0 $\frac{1}{4}$
(蘭,梅) X=1 $\frac{1}{4}$ X=0 $\frac{1}{4}$ X=1 $\frac{1}{4}$ X=0 $\frac{1}{4}$
(蘭,蘭) X=2 $\frac{1}{4}$ X=0 $\frac{1}{4}$ X=1 $\frac{1}{4}$ X=1 $\frac{1}{4}$
我們這個表要說明同一個實驗，可以定義很多不同的函數-隨機變數。 綜合隨機變數的值和概率，我們可以有一種容易運用的概率函數。 上面表中的概率函數和累積概率分佈函數是：
X P(X=x)=ai $\sum_{-\infty}^{N} P(X=x)=P(X\leq N)$
蘭面 $P(X=0)=\frac{1}{4}$ $P(X\leq 0)=\frac{1}{4}$
出現 $P(X=1)=\frac{2}{4}$ $P(X\leq 1)=\frac{3}{4}$
的次數 $P(X=2)=\frac{1}{4}$ $P(X\leq 2)=1$
最少出現 $P(X=0)=\frac{3}{4}$ $P(X\leq 0)=\frac{3}{4}$
二次梅花 $P(X=2)=\frac{1}{4}$ $P(X\leq 2)=1$
最多出現 $P(X=0)=\frac{1}{4}$ $P(X\leq 0)=\frac{1}{4}$
一次梅花 $P(X=1)=\frac{3}{4}$ $P(X\leq 1)=1$
兩面 $P(X=0)=\frac{1}{2}$ $P(X\leq 0)=\frac{1}{2}$
全同 $P(X=1)=\frac{1}{2}$ $P(X\leq 1)=1$
概率函數 累積分佈函數
這裏的例子自然簡單一點，有時在複雜的實驗或煩瑣的要求時， 隨機變數和它的概率函數也相應的複雜起來，我們且不談這些技巧上的問題， 要指出的倒是：我們有成千上萬的隨機變數，每一個都有一個概率函數相隨， 每一個現象或要求可以計算出一個隨機變數出來， 只有滿足幾個簡單條件都可以過關了：

(一)隨機變數的定義值是互不混淆的。

(二)對每一個值都有一個0和1之間的概率函數值與之相對應：
\begin{displaymath}P(X=x_i)=a_i,0\leq a_i \leq 1 \end{displaymath}


(三)隨機變數的累積分佈函數的最小值為0，最大值為1。即是
\begin{displaymath} 0 \leq P(X\leq x) \leq 1 \end{displaymath}

這幾條條件並不太難滿足，因此分佈函數多得很了。 我們回到原來問題想。到現在為止，進展是：我們要解釋一種社會現象， 首先假設可以有一個數學模型(概率空間)來滿足這個要求。為了方便計算， 把這模型用隨機變數這種方式寫出來。也就是說，我們先解答了隨機變數， 然後把這模型寫成為它的分佈函數。 因為社會現象如今可以假設它是一個分佈函數， 或這現象的單元服從某個隨機變數的概率(密度)函數。 (密度函數應用到連續型的隨機變數上面。) 解釋社會現象變為了解它相伴的分佈函數，也就是在這分佈函數中找到「測度」來。
社會現象很多，每一次要分析一個現象，再要重新研究它所相應而生的隨機變數和分佈函數，太麻煩了。 事實上，雖然隨機變數很多，但典型的分佈函數，供我們常用的不外二十個左右， 所以我們不妨先研究一下幾個有代表性的分配函數。以後碰到一個社會現象時， 只要把隨機變數類型認清楚，歸到某一典型的分佈函數， 我們便可以簡單利用已研究清楚的性質和定理了。 典型的分佈函數是


(一)二項分佈函數：(有限離散型)
凡隨機變數有二分型的特性;事件出現的方法非此即彼，非甲即乙，非善即惡……時， 都是屬於這一類的分佈函數。它的概率函數是
\begin{displaymath} P(X=x)=C_x^nP^x(1-P)^{n-x},x=0,1,2,\cdots\cdots,n \end{displaymath}


(二)無限離散型;波爾松型：
凡隨機變數滿足一些條件：


(1)事件發生的概率與（時間）區間長短有關，而與開始或結束地點無關。

(2)現在發生之事件跟過去事件或未來事件無關。

(3)短時期內只出現一簡單事件的概率和區間長度成比例。

(4)短時間內出現多過一簡單事件機會很少。
在這些條件之下，出現了一個波爾松型隨機變數它的概率函數是，
\begin{displaymath} P(X=x)=\frac{e^{-\lambda}(\lambda)^x}{x!} ,x=0,1,2,\cdots\cdots \end{displaymath}


(三)連續型；常態分佈函數：
當樣本數很大，隨機變數所取的值為很多時，適當變換後，有一個理想型的分佈函數出現：
< \infty,-\infty < \mu < \infty,0<\rho \end{displaymath}" width="412" border="0" height="45" />

在普通情形中，大多隨機變數可用這三類型來代表。自然也可以進一步學多幾個不同類形的隨機變數。 如卡方分佈、幾何分佈、Student 分佈

(己)參數

在上面三節中，我們不外在學習一些準備知識，大概來說，我們想這樣做： 一般情況下我們假設某一社會現象服從某一型分佈函數，希望了解這個類型的分佈函數，可以進一步了解分佈函數的內涵。
但是，一個分佈函數裏面仍包涵著幾種特性，出現在概率函數的數學代表式中， 便是它的參數，例如在二項分佈中的P， 在波爾松型分佈的λ，和在常態分佈中的μ和$\rho^2$。
例如在上談到的全年國民收入中，我們可以假設這個收入是一個機隨變數， 它服從一個常態分佈函數（若次數很大，一般情形。用中心極限定理來逼近，說估計量趨近常態分佈也。） 但是我們不知道這個常態分佈函數的參數μ和$\rho^2$是多少，我們仍要下功夫去猜測， 然後才能知道分佈函數，也就是說才知道原來的現象是怎樣。
一般說來，我們回到最原始找測度的問題了。參數是常數，最少也屬於由數據觀點看來的常數， 是可以由數據進而猜測決定的。所有參數皆是由測度決定的，雖然測度有時不止於參數， （例如在無母分析上面。）但參數即使不是單由測度決定，也可以由他的函數所決定。因此， 我們由原始到結束，就說明了目的全在找「測度」， 整個統計就建立在猜測這個測度是什麼這個問題上。
在一個參數分析的方法上，過程是這樣子的： 假設我們所要知道的社會現象是服從某一型(如常態)分佈函數。 我們想確定一下它是一個怎樣子的常態分佈，那麼只要測度出參數是什麼就夠了。 因為參數一定，整個分佈函數就定下來了。
許多情形也可以證明不需要全部應用所有數據，我們只需從母數數據中， 抽出一部份隨機而具代表性的樣本，從這樣來找出一些統計量，來測度那些參數的值。
這樣子已到了統計推論了。推論的意思自然和由小樣本推論到大樣本。 另一方面也是為了利用測度來預測參數乃至整個分佈函數。我們舉推論的常用方法為例。


(一)統計檢定： 統計檢定傳統方法是，先假設參數適合一些條件，如等於某個數值， 然後抽一樣本和利用這樣本計算出一個測度，(由一些理論方法如類似函數比率檢定所找到的檢定統計量)， 把這測度和原先假設的數值比較便可以知道原來假設對不對了。

(二)估計： 估計是直接猜測參數的真值，由抽樣出來的數值，算出一個測度，用它來估計參數的值。 例如在母數的假設為常態分佈時，我們常用樣本算出來的平均值，用來估計母數的數學期望值，即常態分佈中的μ值。又例如我們也會用樣本出來的方差，來估計母數的方差，即常態分佈中的$\rho^2$。
用數學方程式寫出來，我們是說：利用樣本平均數，統計量
\begin{displaymath} \overline{X}=\frac{\sum x_i}{n} \end{displaymath}

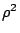（其中xi代表樣本中的數據）用來作測度，來估計母數平均數μ。 或利用樣本方差，統計量 來估計母數方差$\rho^2$
\begin{displaymath} S^2=\frac{\sum (X_i-\overline{X})^2}{n-1} \end{displaymath}

至於為什麼要用$\overline{X}$和S2呢，這裏面就涉及了統計一些原理了。
(庚)小結：
我們總結一下這篇文字的主要內容：統計的主要工作在查詢社會現象，自然現象，為了達到這目的， 只好利用統計方法，找到了適當的統計量，來解釋這現象。初步敘述統計時期， 範圍只限在現象已出現的事件上。這時的測度也只是整理和簡明化測度。 但如果這現象是一個更龐大的事實的表徵，那麼我們可以將這測度普遍化， 用來推論和預測它所能代表的這個龐大的事實的一些意義。這個情形比較複雜， 我們要考慮這龐大的事實的規律性問題，如果可能控制，那麼我們進一步假設它服從某種概率模型； 如果不可能控制，則不能設想它有一個模型，只好就它的一些經驗結果來繼續研究。
目前研究得比較清楚，應用比較多的是假設其服從某些已知的概率模型-分佈函數， 尤其是在數目大的時侯。例如我們可以在龐大的事實現象中，抽到很大的有代表性的樣本， 因此也可以進一步考慮它是否服從常態分佈函數，而我們要找尋到測度，來估計它的參數真值， 或推論及預測整個現象的趨向問題。甚至可以依照某些原則，而作一些決策的打算，例如防止最大的損失， 或看重平均賺錢比較多這一類的的原則，會引導我們的決策函數的判定的。到了這裏， 統計的結構不僅能敘述現象的一堆數據的特性，且能進一步採取某些行動了。
我們也許可以這樣結論；統計的目的在先清楚分析事實的殊相，通過數據和模型，然後再採取行動， 推論事實的真相，特質和預測事實的未來走向。
於

沒有留言:

張貼留言

注意：只有此網誌的成員可以留言。