https://www.facebook.com/hanching.chung/videos/2477397655751748
高中、大學 機率、統計學、田口方法 (實驗計畫)
趙民德博士
地點: 資訊科學研究所402 室
“The Taming of Chance” Ian Hacking, Eminent Philosopher of Science and Much Else, Dies at 87苑舉 正編: Scientific Reason by Ian Hacking/大學生哲學
Professor Hacking’s intellectual scope seemed to know no bounds. Because of his ability to span multiple academic fields, he was often described as a bridge builder.
“Ian Hacking was a one-person interdisciplinary department all by himself,” Cheryl Misak, a philosophy professor at the University of Toronto, said in a phone interview. “Anthropologists, sociologists, historians and psychologists, as well as those working on probability theory and physics, took him to have important insights for their disciplines.”
Image
 Professor Hacking’s book “The Taming of Chance” was named one of the best 100 nonfiction books of the 20th century by the Modern Library.
Professor Hacking’s book “The Taming of Chance” was named one of the best 100 nonfiction books of the 20th century by the Modern Library.Professor Hacking wondered aloud, the interviewer noted, if the whole universe was governed by nonlocality — if “everything in the universe is aware of everything else.”
“That’s what you should be writing about,” he said. “Not me. I’m a dilettante. My governing word is ‘curiosity.’”
Ian Hacking, Eminent Philosopher of Science and Much Else, Dies at 87
Never limited by categories, his free-ranging intellect delved into physics, probability and anthropology, establishing him as a major thinker.
Give this article
 The philosopher Ian Hacking “was a one-person interdisciplinary department all by himself,” a colleague said.Credit...via Jane Frances Hacking
The philosopher Ian Hacking “was a one-person interdisciplinary department all by himself,” a colleague said.Credit...via Jane Frances Hacking| 大 |
| ||||
| 惑 |
| ||||
| 不 |
| ||||
| 解 |
|
解釋:
十分糊塗、迷惑,不懂道理。語本《莊子.天地》:「大惑者終生不解,大愚者終身不靈。」後用以指對事物感到非常疑惑,無法瞭解。宋.陸游〈與趙都大啟〉:「伏念某下愚無知,大惑不解,罪宜永斥。」
終生不解
知新集:談圖表思法的長短,感人的圖表.拿破崙征俄......、戰機上的彈孔數;Abraham Wald、倖存者偏誤(survivorship bias).......《戴明領導手冊》(The Leader's Handbook) vs 《數學教你不犯錯》(How Not to Be Wrong: The Power of Mathematical Thinking) pp.08~17
https://www.facebook.com/hanching.chung/videos/758957232342879
知新集:談圖表思法的長短,感人的圖表.......、戰機上的彈孔數;Abraham Wald、倖存者偏誤(survivorship bias).......《戴明領導手冊》(The Leader's Handbook) vs 《數學教你不犯錯》(How Not to Be Wrong: The Power of Mathematical Thinking) pp.08~17
知新集:談圖表思法的長短,感人的圖表.......、戰機上的彈孔數.......《戴明領導手冊》(The Leader's Handbook) vs 《數學教你不犯錯》(How Not to Be Wrong: The Power of Mathematical Thinking)
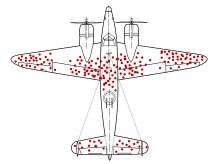
2023年3月17日晨,用Google 查Abraham Wald,即有飛機彈孔圖.....
沃德·亞伯拉罕(匈牙利語:Wald Ábrahám;1902年10月31日-1950年12月13日)匈牙利數學家、美國哥倫比亞大學教授,在決策論、幾何學、計量經濟學等方面有所貢獻,第二次世界大戰期間為美國海軍服務,發現倖存者偏差。
生平[編輯]
倖存者偏差[1][2]或倖存者偏誤(英語:survivorship bias),也稱為生存者偏差[3],是一種邏輯謬誤,屬於選擇偏差的一種。當過度關注「倖存」的人事物,從而造成忽略那些沒有倖存的(也可能因為無法觀察到),便會得出錯誤的結論。
概要[編輯]
生存偏見可能導致過度樂觀的信念,因為失敗被忽略,例如當不再存在的公司被排除在財務業績分析之外時。它也可能導致他人誤認一個群體的成功具有一些特殊屬性,而不僅僅是巧合(相關證明了因果關係)。其謬論形式為:倖存過程B的個體A有特性C,因此任何個體倖存過程B需要有特性C。有特性C但無法倖存過程B的個體被忽略不加以討論。邏輯偏差在於只關注篩選結果做出評估,而忽略篩選條件與篩選機制等資訊。用俗語「死人不會說話」來解釋其成因意指當取得資訊之管道,僅來自於倖存者時(因為無從由死者/淘汰者/離場者獲得來源),此資訊可能會存在與實際情況不同之偏差。這種偏差可以導致各種錯誤結論。
案例[編輯]
軍事[編輯]
第二次世界大戰期間的1941年,美國哥倫比亞大學統計學亞伯拉罕·沃德教授接受美國海軍的要求,運用他在統計方面的專業知識給出關於『飛機應該如何加強防護,才能降低被炮火擊落的機率』的建議。沃德教授針對盟軍的轟炸機遭受攻擊後的相關數據,進行分析和研究後發現:機翼是整個飛機中最容易遭受攻擊的位置,而發動機則是最少被攻擊的位置。因此美國海軍指揮官認為『應該加強機翼的防護,因為這是最容易被擊中的位置』,但是沃德教授給出的結論是『我們應該強化發動機的防護』。
沃德教授提出以下其加強機身防護意見的依據:
- 本次統計的樣本,僅包含沒有因敵火射擊而墜毀並安全返航的轟炸機。
- 沃德教授假設所有中彈的彈著點應該會平均分布在機身各處,而能安全返航的轟炸機機身中彈數量較多的區域,是即使被擊中也比較不會導致墜機的部位。
- 機翼被擊中很多次的轟炸機,大多數仍然能夠安全返航。
- 發動機彈孔較少的原因並非真的不容易中彈,而是一旦中彈,其生還並安全返航的可能性就微乎其微。
軍方最終採取了教授提出的增加發動機防護的建議,後來證實該決策是完全正確的。這項研究對當時仍在發展初期的作業研究領域具有深遠的影響。[4]
https://en.wikipedia.org › wiki › Abraham_Wald
Abraham Wald was a Jewish Hungarian mathematician who contributed to decision theory, geometry, and econometrics and founded the field of statistical ...
《數學教你不犯錯》pp.08~17
Abraham Wald and the Missing Bullet Holes
An excerpt from How Not To Be Wrong by Jordan Ellenberg
This story, like many World War II stories, starts with the Nazis hounding a Jew out of Europe and ends with the Nazis regretting it. Abraham Wald was born in 1902 in what was then the city of Klausenburg in what was then the Austro-Hungarian Empire. By the time Wald was a teenager, one world war was in the books and his hometown had become Cluj, Romania. He was the grandson of a rabbi and the son of a kosher baker, but the younger Wald was a mathematician almost from the start. His talent for the subject was quickly recognized, and he was admitted to study mathematics at the University of Vienna, where he was drawn to subjects abstract and recondite even by the standards of pure mathematics: set theory and metric spaces.
But when Wald’s studies were completed, it was the mid-1930s, Austria was deep in economic distress, and there was no possibility that a foreigner could be hired as a professor in Vienna. Wald was rescued by a job offer from Oskar Morgenstern. Morgenstern would later immigrate to the United States and help invent game theory, but in 1933 he was the director of the Austrian Institute for Economic Research, and he hired Wald at a small salary to do mathematical odd jobs. That turned out to be a good move for Wald: his experience in economics got him a fellowship offer at the Cowles Commission, an economic institute then located in Colorado Springs. Despite the ever-worsening political situation, Wald was reluctant to take a step that would lead him away from pure mathematics for good. But then the Nazis conquered Austria, making Wald’s decision substantially easier. After just a few months in Colorado, he was offered a professorship of statistics at Columbia; he packed up once again and moved to New York.
And that was where he fought the war.
The Statistical Research Group (SRG), where Wald spent much of World War II, was a classified program that yoked the assembled might of American statisticians to the war effort — something like the Manhattan Project, except the weapons being developed were equations, not explosives. And the SRG was actually in Manhattan, at 401 West 118th Street in Morningside Heights, just a block away from Columbia University. The building now houses Columbia faculty apartments and some doctor’s offices, but in 1943 it was the buzzing, sparking nerve center of wartime math. At the Applied Mathematics Group−Columbia, dozens of young women bent over Marchant desktop calculators were calculating formulas for the optimal curve a fighter should trace out through the air in order to keep an enemy plane in its gunsights. In another apartment, a team of researchers from Princeton was developing protocols for strategic bombing. And Columbia’s wing of the atom bomb project was right next door.
But the SRG was the most high-powered, and ultimately the most influential, of any of these groups. The atmosphere combined the intellectual openness and intensity of an academic department with the shared sense of purpose that comes only with high stakes. “When we made recommendations,” W. Allen Wallis, the director, wrote, “frequently things happened. Fighter planes entered combat with their machine guns loaded according to Jack Wolfowitz’s (Paul’s dad)recommendations about mixing 5 types of ammunition, and maybe the pilots came back or maybe they didn’t. Navy planes launched rockets whose propellants had been accepted by Abe Girshick’s sampling-inspection plans, and maybe the rockets exploded and destroyed our own planes and pilots or maybe they destroyed the target.”
The mathematical talent at hand was equal to the gravity of the task. In Wallis’s words, the SRG was “the most extraordinary group of statisticians ever organized, taking into account both number and quality.” Frederick Mosteller, who would later found Harvard’s statistics department, was there. So was Leonard Jimmie Savage, the pioneer of decision theory and great advocate of the field that came to be called Bayesian statistics. (Savage was almost totally blind, able to see only out of one corner of one eye, and at one point spent six months living only on pemmican in order to prove a point about Arctic exploration. Just thought that was worth mentioning.) Norbert Wiener, the MIT mathematician and the creator of cybernetics, dropped by from time to time. This was a group where Milton Friedman, the future Nobelist in economics, was often the fourth-smartest person in the room.
The smartest person in the room was usually Abraham Wald. Wald had been Allen Wallis’s teacher at Columbia, and functioned as a kind of mathematical eminence to the group. Still an “enemy alien,” he was not technically allowed to see the classified reports he was producing; the joke around SRG was that the secretaries were required to pull each sheet of notepaper out of his hands as soon as he was finished writing on it. Wald was, in some ways, an unlikely participant. His inclination, as it always had been, was toward abstraction, and away from direct applications. But his motivation to use his talents against the Axis was obvious. And when you needed to turn a vague idea into solid mathematics, Wald was the person you wanted at your side.
So here’s the question. You don’t want your planes to get shot down by enemy fighters, so you armor them. But armor makes the plane heavier, and heavier planes are less maneuverable and use more fuel. Armoring the planes too much is a problem; armoring the planes too little is a problem. Somewhere in between there’s an optimum. The reason you have a team of mathematicians socked away in an apartment in New York City is to figure out where that optimum is.
The military came to the SRG with some data they thought might be useful. When American planes came back from engagements over Europe, they were covered in bullet holes. But the damage wasn’t uniformly distributed across the aircraft. There were more bullet holes in the fuselage, not so many in the engines.

The officers saw an opportunity for efficiency; you can get the same protection with less armor if you concentrate the armor on the places with the greatest need, where the planes are getting hit the most. But exactly how much more armor belonged on those parts of the plane? That was the answer they came to Wald for. It wasn’t the answer they got.
The armor, said Wald, doesn’t go where the bullet holes are. It goes where the bullet holes aren’t: on the engines.
Wald’s insight was simply to ask: where are the missing holes? The ones that would have been all over the engine casing, if the damage had been spread equally all over the plane? Wald was pretty sure he knew. The missing bullet holes were on the missing planes. The reason planes were coming back with fewer hits to the engine is that planes that got hit in the engine weren’t coming back. Whereas the large number of planes returning to base with a thoroughly Swiss-cheesed fuselage is pretty strong evidence that hits to the fuselage can (and therefore should) be tolerated. If you go to the recovery room at the hospital, you’ll see a lot more people with bullet holes in their legs than people with bullet holes in their chests. But that’s not because people don’t get shot in the chest; it’s because the people who get shot in the chest don’t recover.
Here’s an old mathematician’s trick that makes the picture perfectly clear: set some variables to zero. In this case, the variable to tweak is the probability that a plane that takes a hit to the engine manages to stay in the air. Setting that probability to zero means a single shot to the engine is guaranteed to bring the plane down. What would the data look like then? You’d have planes coming back with bullet holes all over the wings, the fuselage, the nose — but none at all on the engine. The military analyst has two options for explaining this: either the German bullets just happen to hit every part of the plane but one, or the engine is a point of total vulnerability. Both stories explain the data, but the latter makes a lot more sense. The armor goes where the bullet holes aren’t.
Wald’s recommendations were quickly put into effect, and were still being used by the navy and the air force through the wars in Korea and Vietnam. I can’t tell you exactly how many American planes they saved, though the data-slinging descendants of the SRG inside today’s military no doubt have a pretty good idea. One thing the American defense establishment has traditionally understood very well is that countries don’t win wars just by being braver than the other side, or freer, or slightly preferred by God. The winners are usually the guys who get 5% fewer of their planes shot down, or use 5% less fuel, or get 5% more nutrition into their infantry at 95% of the cost. That’s not the stuff war movies are made of, but it’s the stuff wars are made of. And there’s math every step of the way.
Why did Wald see what the officers, who had vastly more knowledge and understanding of aerial combat, couldn’t? It comes back to his math-trained habits of thought. A mathematician is always asking, “What assumptions are you making? And are they justified?” This can be annoying. But it can also be very productive. In this case, the officers were making an assumption unwittingly: that the planes that came back were a random sample of all the planes. If that were true, you could draw conclusions about the distribution of bullet holes on all the planes by examining the distribution of bullet holes on only the surviving planes. Once you recognize that you’ve been making that hypothesis, it takes only a moment to realize it’s dead wrong; there’s no reason at all to expect the planes to have an equal likelihood of survival no matter where they get hit. In a piece of mathematical lingo we’ll come back to in chapter 15, the rate of survival and the location of the bullet holes are correlated.
Wald’s other advantage was his tendency toward abstraction. Wolfowitz, who had studied under Wald at Columbia, wrote that the problems he favored were “all of the most abstract sort,” and that he was “always ready to talk about mathematics, but uninterested in popularization and special applications.”
Wald’s personality made it hard for him to focus his attention on applied problems, it’s true. The details of planes and guns were, to his eye, so much upholstery — he peered right through to the mathematical struts and nails holding the story together. Sometimes that approach can lead you to ignore features of the problem that really matter. But it also lets you see the common skeleton shared by problems that look very different on the surface. Thus you have meaningful experience even in areas where you appear to have none.
To a mathematician, the structure underlying the bullet hole problem is a phenomenon called survivorship bias. It arises again and again, in all kinds of contexts. And once you’re familiar with it, as Wald was, you’re primed to notice it wherever it’s hiding.
Like mutual funds. Judging the performance of funds is an area where you don’t want to be wrong, even by a little bit. A shift of 1% in annual growth might be the difference between a valuable financial asset and a dog. The funds in Morningstar’s Large Blend category, whose mutual funds invest in big companies that roughly represent the S&P 500, look like the former kind. The funds in this class grew an average of 178.4% between 1995 and 2004: a healthy 10.8% per year (To be fair, the S&P 500 index itself did even better, gaining 212.5% over the same period). Sounds like you’d do well, if you had cash on hand, to invest in those funds, no?
Well, no. A 2006 study by Savant Capital shone a somewhat colder light on those numbers. Think again about how Morningstar generates its number. It’s 2004, you take all the funds classified as Large Blend, and you see how much they grew over the last ten years.
But something’s missing: the funds that aren’t there. Mutual funds don’t live forever. Some flourish, some die. The ones that die are, by and large, the ones that don’t make money. So judging a decade’s worth of mutual funds by the ones that still exist at the end of the ten years is like judging our pilots’ evasive maneuvers by counting the bullet holes in the planes that come back. What would it mean if we never found more than one bullet hole per plane? Not that our pilots are brilliant at dodging enemy fire, but that the planes that got hit twice went down in flames.
The Savant study found that if you included the performance of the dead funds together with the surviving ones, the rate of return dropped down to 134.5%, a much more ordinary 8.9% per year. More recent research backed that up: a comprehensive 2011 study in the Review of Finance covering nearly 5,000 funds found that the excess return rate of the 2,641 survivors is about 20% higher than the same figure recomputed to include the funds that didn’t make it. The size of the survivorship effect might have surprised investors, but it probably wouldn’t have surprised Abraham Wald.
沒有留言:
張貼留言
注意:只有此網誌的成員可以留言。